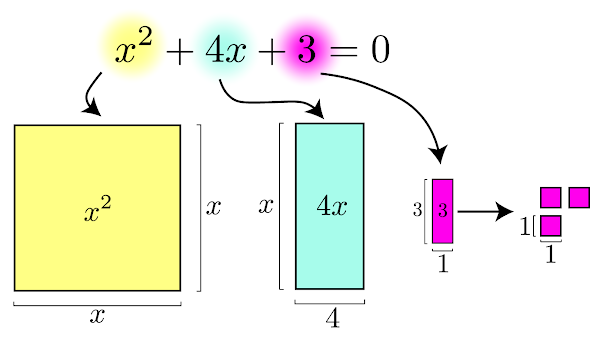
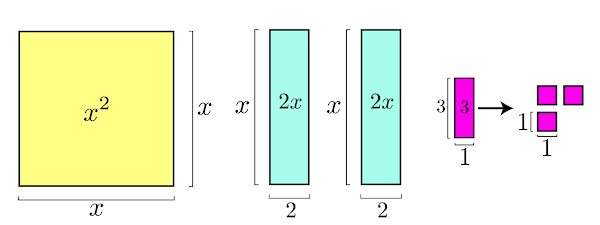
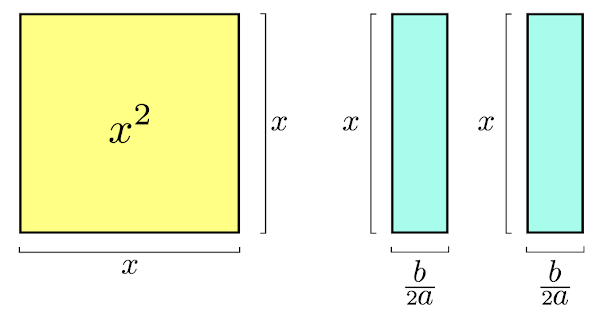
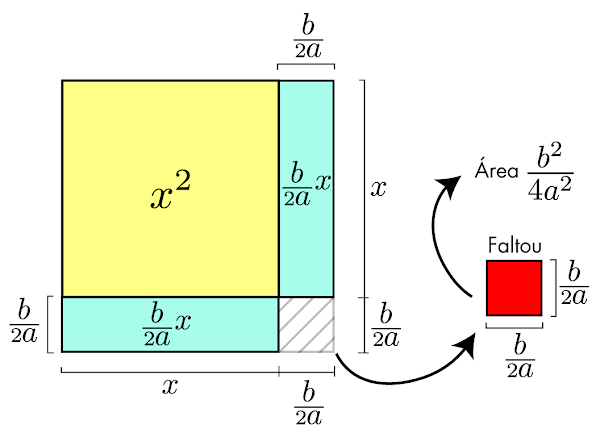
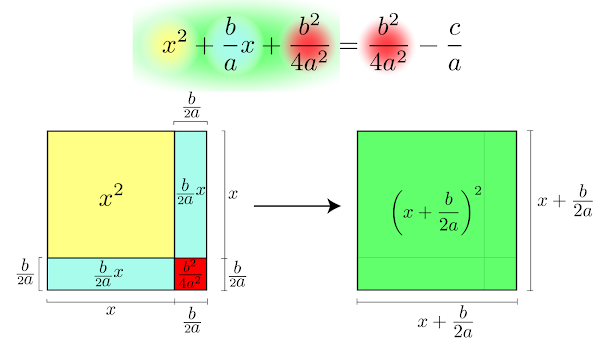
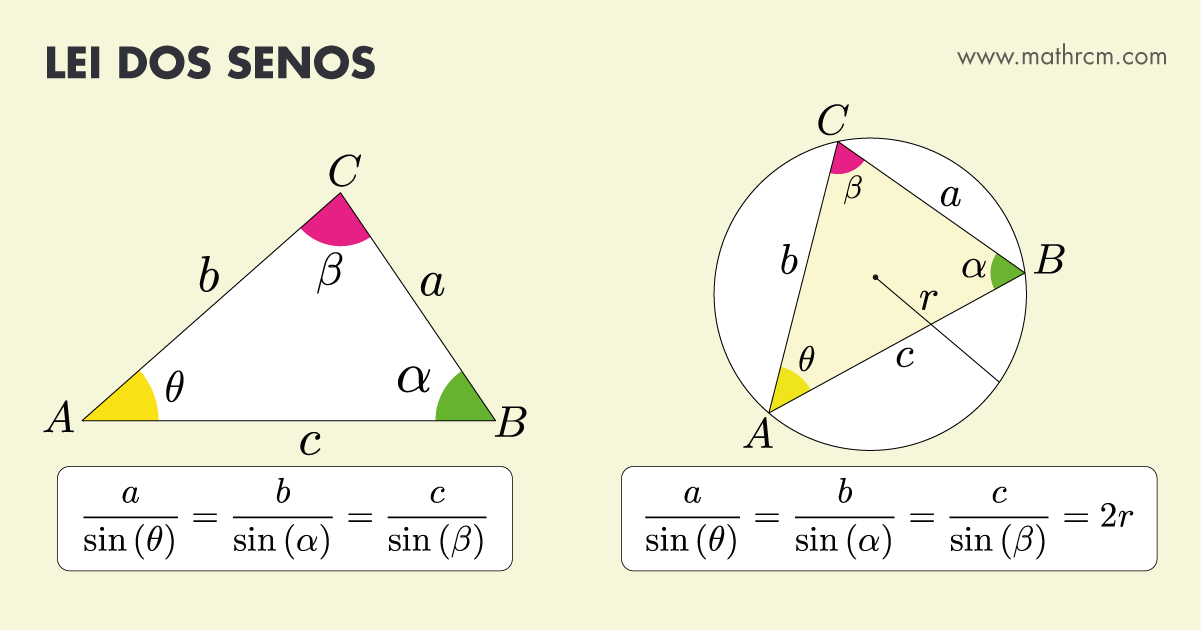
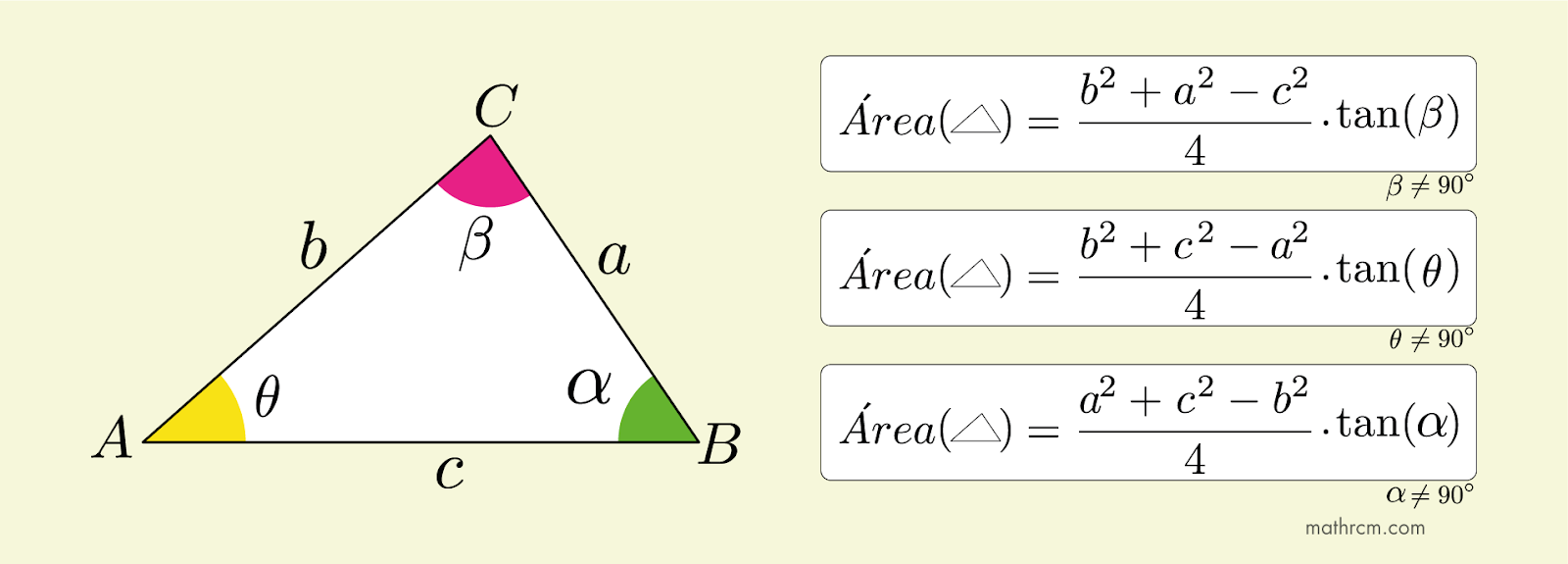
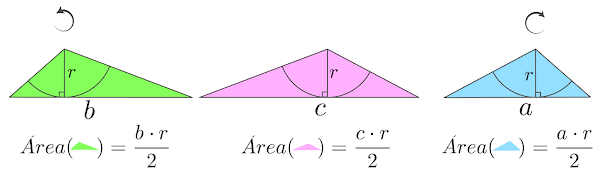
Como calcular as medidas dos ângulos internos de um triângulo, sem usar a função inversa arccos, em função dos seus lados. A fórmula que criei em 2023, ou pelo menos cheguei a ela de forma independente, uma vez que nunca tinha visto tal fórmula em nenhum outro local. Aqui está a fórmula dos radicais aninhados com 5 e 2 interações respectivamente.
\begin{equation}
\theta = \frac{180\cdot 2^{5}}{\pi}\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}}
\label{eq:radAni01}
\end{equation}
\begin{equation}
\theta = \frac{180\cdot 2^{2}}{\pi}\sqrt{2-\sqrt{2+\sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}
\label{eq:radAni02}
\end{equation}
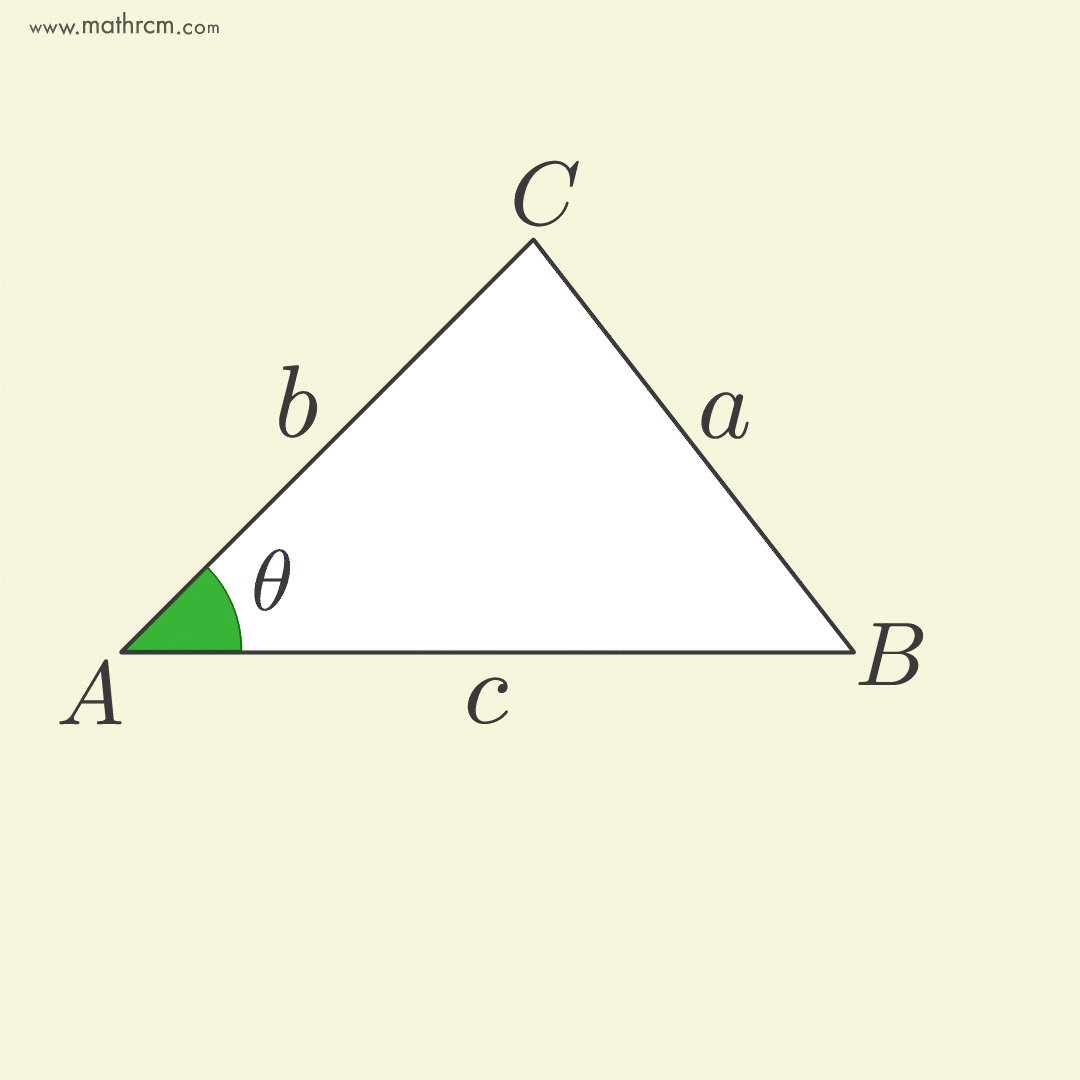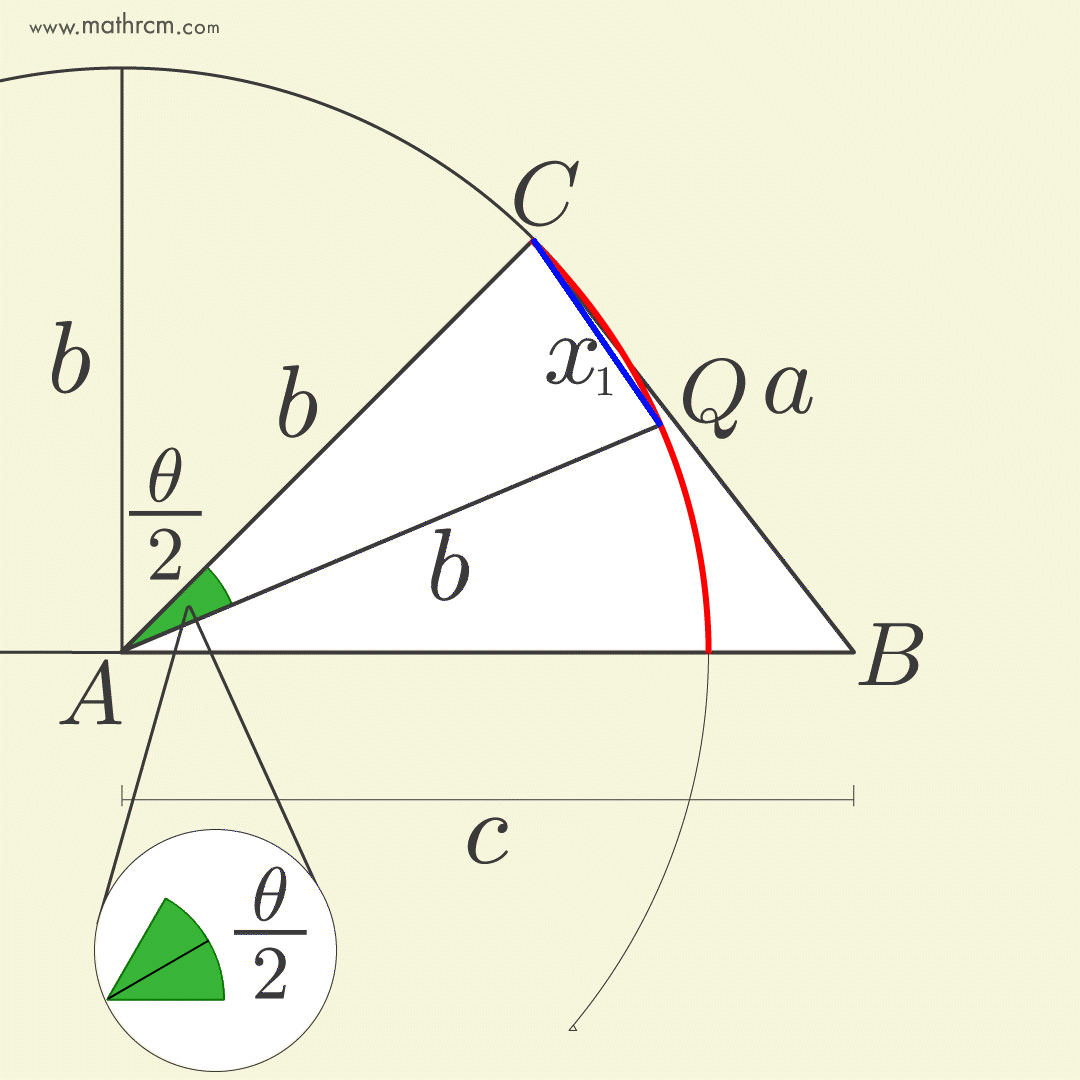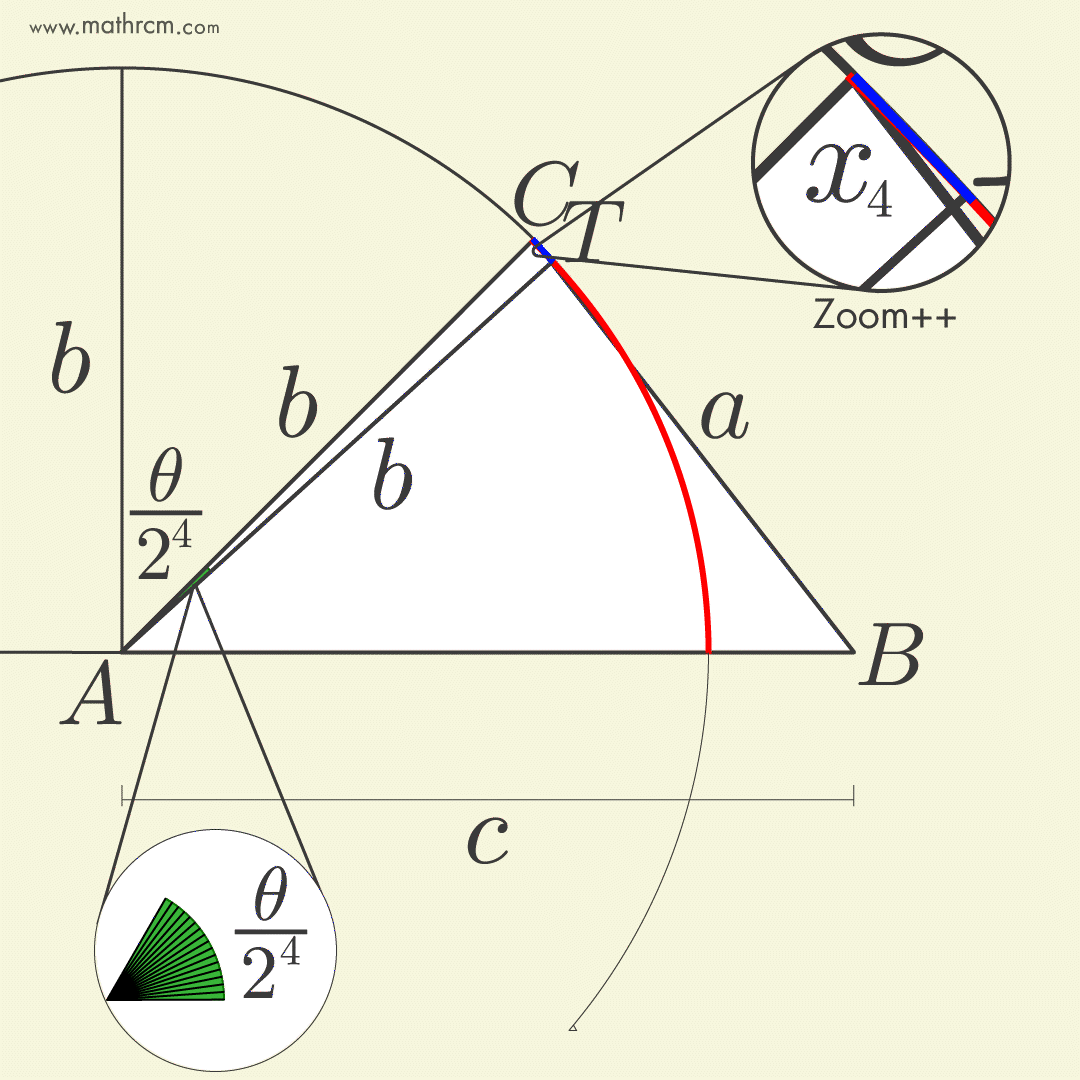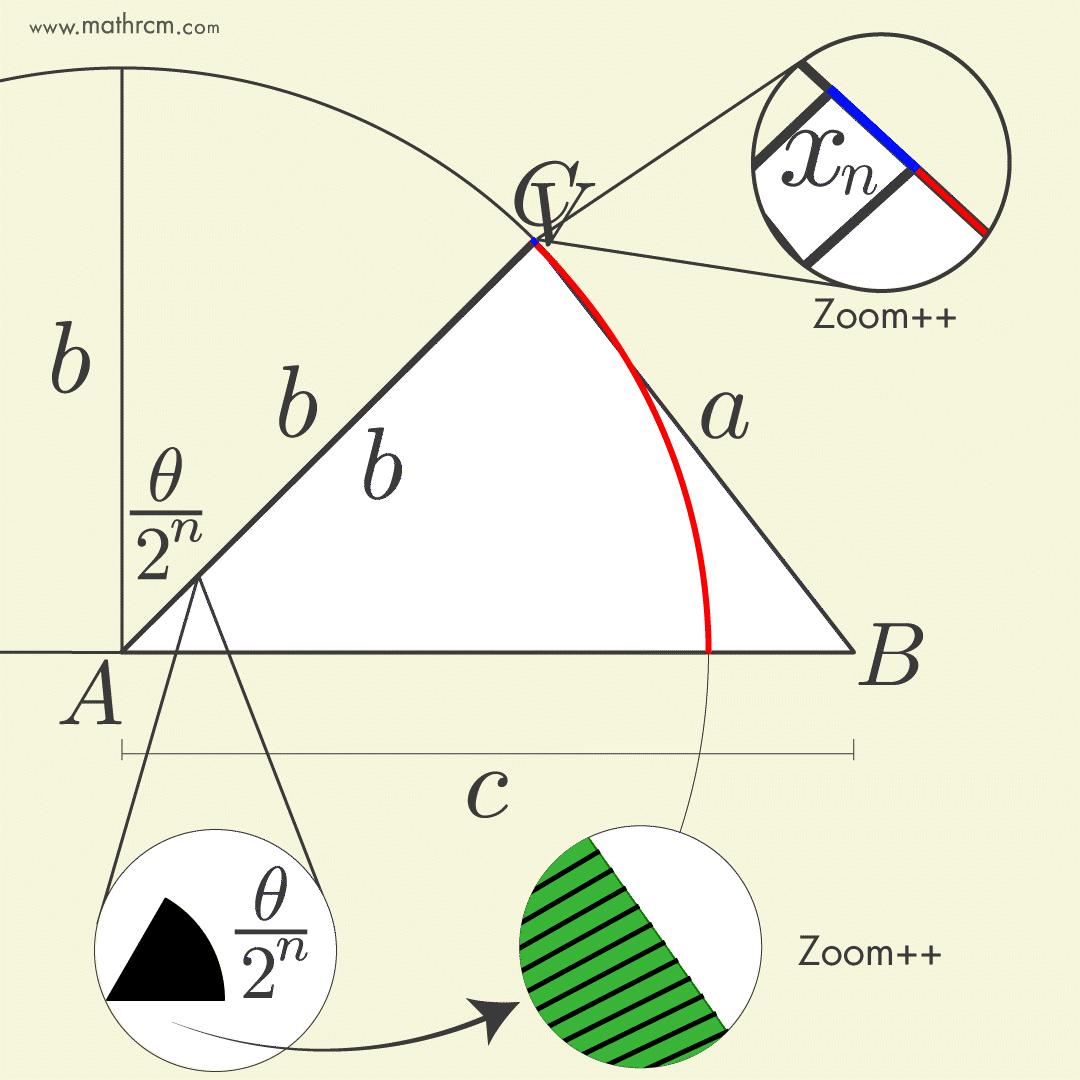
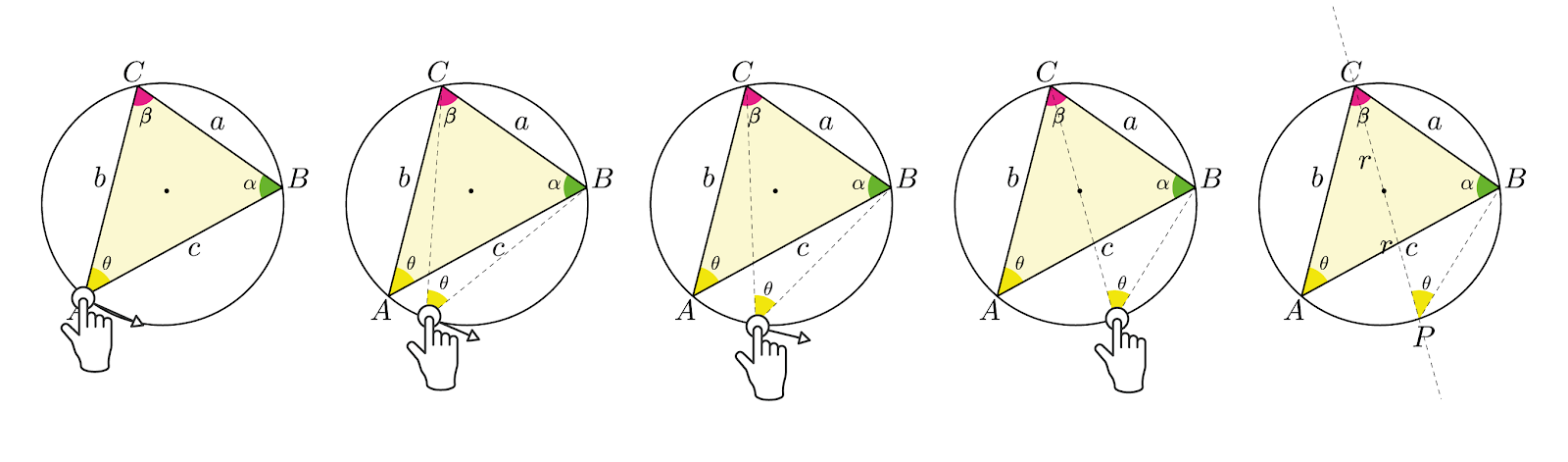
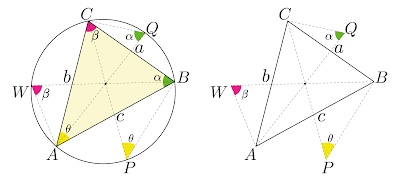
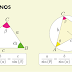
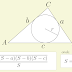
A dedução é bem simples e consiste em reduzir o segmento (azul) até coincidir com uma pequena parte do arco (vermelho) de uma circunferência com centro no vértice \(A\) e raio igual a um dos lados adjacentes ao ângulo escolhido, ao mesmo tempo que o ângulo \(\theta\) é fatiado em partes iguais. A demosntração completa está disponível no site O Baricentro da Mente de Kleber Kilhian.
O raciocínio principal pode ser observado na animação abaixo. Aguarde o carregamento...
O \(\cos \left( \frac{\theta}{2^n} \right)\) pode ser recuperado pela fórmula do cosseno do arco metade e o comprimento do segmento azul \(x\) pode ser obtido pela lei dos cossenos. Juntando tudo, obtemos uma estranha fórmula de radicais aninhados.
\(\require{gensymb}\)
Pontos importantes
- A raio da circunferência poder ser qualquer um dos lados adjacentes ao ângulo escolhido.
- A cada ação de dividir ao meio o ângulo resultante (lê-se iteração) deixa a fórmula mais precisa.
- Se todos os ângulos tendem a \(60 \degree\), menos interações são necessárias, assim como ângulos pequenos.
- Caso o ângulo tenda a \(180 \degree\), ao menos 7 interações são necessárias para uma boa precisão.
A busca pela fórmula na internet
Logo após chegar à fórmula dos radicais aninhados, comecei a procurar na internet por uma fórmula igual e até a data da publicação deste poste não encontrei nenhuma fórmula igual e/ou que utilize o método. No entanto, encontrei a fórmula de Viète\(^2\) para calcular o valor de \(\pi\).
\begin{equation}
\pi = \lim_{k \to \infty}2^k \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\cdot \cdot \cdot+\sqrt{2}}}}}}
\label{eq:radAni03}
\end{equation}
Unificando as duas fórmulas. Substituindo \(\pi\) na fórmula dos radicais aninhandos.
\begin{equation}
\theta = 180 \frac{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\cdot \cdot \cdot+\sqrt{\frac{(a+b+c)(b+c-a)}{bc}}}}}}}}{\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\cdot \cdot \cdot+\sqrt{2}}}}}}}
\label{eq:radAni04}
\end{equation}
@rodrigo_cstm Fórmula para calcular as medidas dos ângulos internos de um triângulo qualquer em função dos lados. #angulos #math #matematica #triangle #triangulo #angulosinternosdotriangulo ♬ som original - Rodrigo
Notas e referências
- \(^1\) Fórmula para calcular as medidas dos ângulos internos de um triângulo qualquer em função de seus lados. Publicado por Kleber Kilhian em 09/06/2023. URL: https://www.obaricentrodamente.com/2023/06/formula-para-calcular-as-medidas-dos-angulos-internos-de-um-triangulo-qualquer-em-funcao-de-seus-lados.html.
- \(^2\) Viète's formula. From Wikipedia, the free encyclopedia. URL: https://en.wikipedia.org/wiki/Vi%C3%A8te%27s_formula.